浙大_数据结构_第一讲_基本概念_笔记
1.1 什么是数据结构
数据结构(Data Structure)是计算机中存储,组织数据的方式. 通常情况下,精心选择的数据结构可以带来最优效率的算法.
—维基百科
1.1.1 图书存放方式的例子说明:
####结论: 解决问题方法的效率跟数据的组织方式有关.
1.1.2 关于空间的使用

结果: N取大值时递归由于占用过多资源直接报错.所以要谨慎使用递归.

结果: 第一种不如第二种先采用结合律有内往外算的方法.
Tips: C语言clock()函数计算运行时钟打点示例
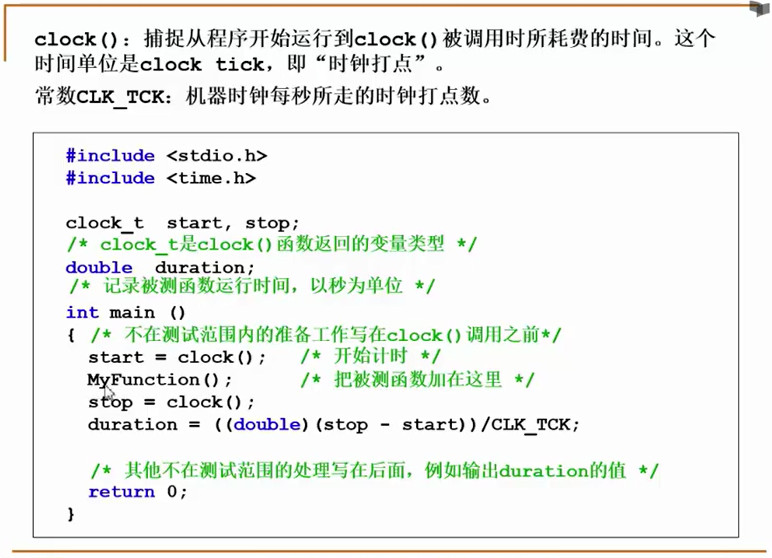
结论: 解决问题方法的效率还跟算法的巧妙程度有关.
1.1.4 抽象数据类型
所以到底什么是数据结构
数据对象在计算机中的组织方式
逻辑结构
线性结构[^一对一]和树形结构[^一对多]和图的结构[^多对多]
物理存储结构
用
抽象数据类型(Abstract Data Type)来描述
数据对象必定与一系列加在其上的操作相关联
完成这些操作所用的方法就是算法
抽象数据类型(Abstract Data Type)
数据类型
- 数据对象集
- 数据集合相关联的操作集
- 抽象: 描述数据类型的方法不依赖于具体实现
tips: 数据对象集和操作级在C语言里是独立处理的.而在面向对象语言里往往封装在一个类里.
抽象数据类型举例

1.2 什么是算法
1.2.1
定义:
- 算法(Algorithm)
- 一个有限的指令集
- 接受一些是输入(可选)
- 产生输出
- 一定在有限步骤后终止
- 每一条指令必须
- 有充分明确的目标,无歧义
- 计算机处理能力之内
- 描述不依赖于任何一种计算机语言和具体的实现手段
描述不依赖于任何一种计算机语言和具体的实现手段 伪代码举例

1.2.2 什么是好的算法
空间复杂度 S(n)
根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断。
时间复杂度 T(n)
根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。
回顾 前面1.1.2 :
递归和循环两种计算printN方法的空间复杂度区别;
计算多项式两种方法的时间复杂度区别(由于计算机计算加减法远快于乘除法,所以这里采用计算做了多少次乘法就可以衡量时间复杂度).
在分析一般算法的效率时,我们一般关注下面两种复杂度
- 最坏情况复杂度 $$T_{worst}$$
- 平均复杂度 $$T_{avg}(n)$$
$T_{avg}(n)$ <= $T_{worst}(n)$
1.2.3 复杂度的渐进表示法

T(n)=O(f(n)) 表示f(n)是T(n)的某种上界
T(n)=G(f(n)) 表示f(n)是T(n)的某种下界
T(n)=Θ(f(n)) 表示f(n)既是上界又是下界,f(n)与T(n)几乎是等价的
Theta(大写Θ,小写θ)
复杂度分析的小窍门

1.3 应用实例:最大子列和问题
算法1

分析可以发现其实没必要单独做k循环,因为j循环里后一项都是前面一项加上A[j]
算法2

一个小技巧:当发现算法复杂度是$$O(N^2)$$ 会想着能不能转换为O(n* log n)
算法3 (感觉比较糊,看最后附上的代码吧 )
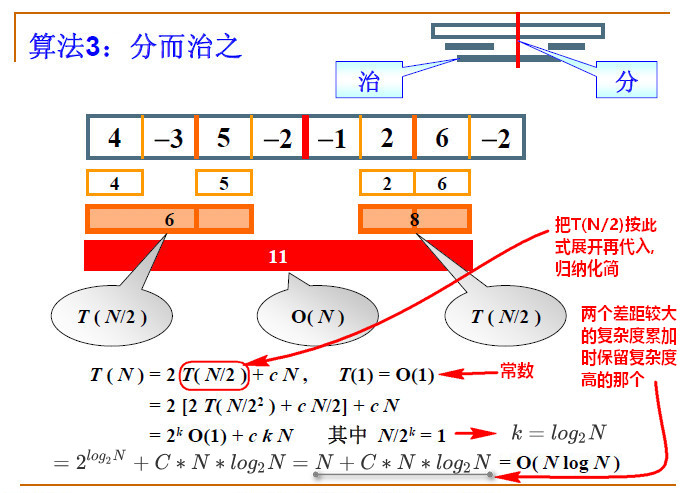
思路:多次一分为二,分别找出左侧的最大子列和与右侧的最大子列和以及跨越边界的最大子列和,比较得出最大的值(图里最大子列和是11).
注意理解: 跨越边界子列和是指一条边界(不管第几级的边界)两边的范围内最大的子列和,边界必须包含在内.类似一个包含此级边界但不超过上一级边界的滑动窗口—这个比较难理解.
分析复杂度:
左侧和右侧的最大子列复杂度都是T(N/2)这个无疑问.
跨越中间边界线子列的复杂度是因为它是分别计算最大一级边界线左边的最大值和右边的最大值,然后加起来,相当于N个值每个值都只扫了一遍.复杂度为N.
(往一边扫描方法:直接不断由边界线向左扫描累加,每次加完判断子列和是否大于暂存的局部最大子列,注意若子列和的最终返回值为负数时返回值置零,避免影响下一步上一级边界线两边的累加)
算法4

从左往右处理,只要值为负数就归零在重新继续算,不为负数时才计算累加后的值比原来的最大值大还是小.之所以叫做在线处理,是因为当它扫描到从左往右的第N个数时,它一定是已扫描部分的最大子列和,即局部的真解.
第三种算法比较难懂,附上老师给的代码来理解:
1 | int Max3( int A, int B, int C ) |